Tabela-Verdade, onde utilizarei isto em minha vida? Parte II

No blog anterior (caso não tenha lido, acesse aqui https://www.maxieduca.com.br/blog/tabela-verdade-uso/) vimos que para a construção de uma tabela verdade precisamos de toda uma estruturação prévia, vimos também que devemos sempre ser possível atribuir um valor lógico: verdadeiro (V) ou falso (F) e que para utilizar a tabela verdade precisamos de proposições compostas.
Agora iremos enfim atribuir valores V ou F, mas para isso devemos entender os operadores lógicos (conjunções, disjunções, condicional e bicondicional) e construção de linhas de uma tabela verdade.
Construção da tabela verdade de uma proposição composta
Vamos começar contando o número de proposições simples que a integram. Se há n proposições simples componentes, então temos 2n linhas. Feito isso, atribuímos a 1ª proposição simples “p1” 2n / 2 = 2n -1 valores V , seguidos de 2n – 1 valores F, e assim por diante.
Exemplos
Se Luciana estuda e João bebe, então Carlos não dança. Observe que temos uma proposição composta formada por 3 proposições simples, logo o número de linhas de nossa tabela será 2³ = 8 linhas, das quais a primeira proposição simples será 23 / 2 = 23 -1 = 2² = 4 valores V seguidos de 4 valores de F.
A segunda proposição simples terá 2n-2 = 23-2 = 2¹ = 2 valores de V seguidos de 2 valores de F, seguidos de 2 valores de V, se alternando entre V e F até preencher as 8 linhas de nossa tabela.
A terceira proposição simples terá 2n-3 = 23-3 = 20 = 1 valor de V depois 1 valor de F, se repetindo até completar as 8 linhas de nossa tabela.
Vou explicar montando uma tabela, então:
Seja a proposição composta:
Se Luciana estuda e João bebe, então Carlos não dança, vou atribuir letras para cada proposição simples:
p = Luciana estuda
q = João bebe
r = Carlos dança
~r = Carlos não dança (adiante veremos como negar uma proposição).
Portanto nossa tabela seguirá nos moldes acima.
Agora devemos entender os operadores lógicos.
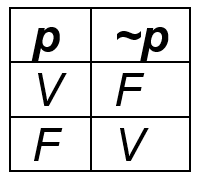
Negação: chamamos de negação de uma proposição representada por “não p” cujo valor lógico é verdade (V) quando p é falsa e falsidade (F) quando p é verdadeira. Assim “não p” tem valor lógico oposto daquele de p.
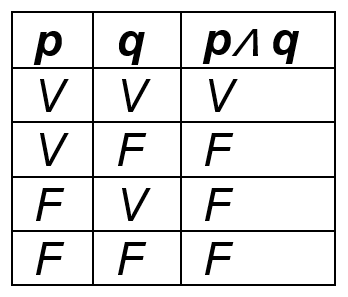
Conjunção: chama-se de conjunção de duas proposições p e q a proposição representada por “p e q”, cujo valor lógico é verdade (V) quando as proposições, p e q, são ambas verdadeiras e falsidade (F) nos demais casos.
Simbolicamente temos: “p ^ q” (lê-se: “p E q”).
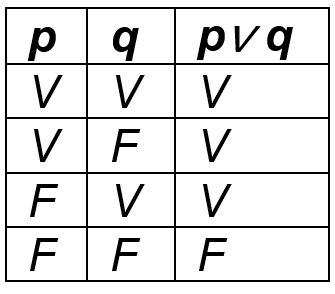
Disjunção simples: chama-se de disjunção inclusiva de duas proposições p e q a proposição representada por “p ou q”, cujo valor lógico é verdade (V) quando pelo menos uma das proposições, p e q, é verdadeira e falsidade (F) quando ambas são falsas.
Simbolicamente: “p v q” (lê-se: “p OU q”).
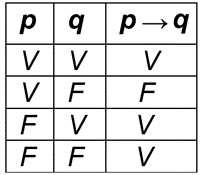
Condicional: chama-se proposição condicional ou apenas condicional representada por “se p então q”, cujo valor lógico é falsidade (F) no caso em que p é verdade e q é falsa e a verdade (V) nos demais casos. Simbolicamente: “p → q” (lê-se: p é condição suficiente para q; q é condição necessária para p). p é o antecedente e q o consequente e “→” é chamado de símbolo de implicação.
Bicondicional: chama-se proposição bicondicional ou apenas bicondicional representada por “p se e somente se q”, cujo valor lógico é verdade (V) quando p e q são ambas verdadeiras ou falsas e a falsidade (F) nos demais casos. Simbolicamente: “p ↔ q” (lê-se: p é condição necessária e suficiente para q; q é condição necessária e suficiente para p).
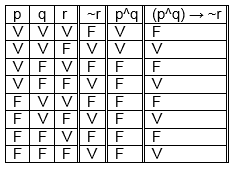
Lembram do nosso exemplo onde eu atribui letras para cada uma das proposições simples? Observem como ele ficará:
(p^q) → ~r, assim sendo, para resolver, primeiro iremos pelo parêntesis, e depois a implicação, vamos lá!
Outro exemplo:
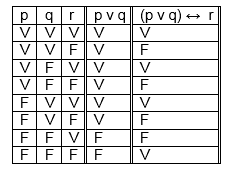
Estéfano é eletricista ou Emerson é matemático , se e somente se, Alberto torce para o São Paulo.
p= Estéfano é eletricista
q = Emerson é matemático
r = Alberto torce para o São Paulo
(p v q) ↔ r, assim sendo, para resolver, primeiro faremos o parêntesis(Disjunção simples) e depois a bicondicional.
Mas antes, iremos resolver o exercício deixado no blog anterior.
1. Analisando as alternativas temos:
(A) Frases interrogativas não são consideradas proposições.
(B) O sujeito aqui é indeterminado, logo não podemos definir quem é ele.
(C) Trata-se de uma proposição composta
(D) É uma frase declarativa onde podemos identificar o sujeito da frase e atribuir a mesma um valor lógico, logo é uma proposição simples.
2. Analisando as alternativas temos:
(A) Não é uma oração composta de sujeito e predicado.
(B) É uma frase imperativa/exclamativa, logo não é proposição.
(C) É uma frase que expressa ordem, logo não é proposição.
(D) É uma frase interrogativa.
(E) Composta de sujeito e predicado, é uma frase declarativa e podemos atribuir a ela valores lógicos, logo é uma proposição.
Vamos exercitar a mente???
1. (MEC – Conhecimentos básicos para os Postos 9,10,11 e 16 – CESPE)
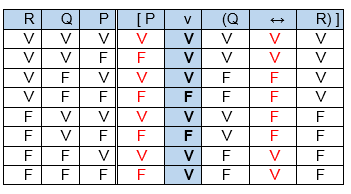
 A figura acima apresenta as colunas iniciais de uma tabela-verdade, em que P, Q e R representam proposições lógicas, e V e F correspondem, respectivamente, aos valores lógicos verdadeiro e falso.Com base nessas informações e utilizando os conectivos lógicos usuais, julgue o item subsecutivo
A figura acima apresenta as colunas iniciais de uma tabela-verdade, em que P, Q e R representam proposições lógicas, e V e F correspondem, respectivamente, aos valores lógicos verdadeiro e falso.Com base nessas informações e utilizando os conectivos lógicos usuais, julgue o item subsecutivo
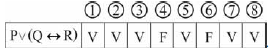
A última coluna da tabela-verdade referente à proposição lógica P v (Q↔R) quando representada na posição horizontal é igual a
( ) Certo ( ) Errado
2. (TRE-RJ – Analista Judiciário – CONSULPLAN/2017) De acordo com algumas implicações lógicas, analise as afirmativas a seguir.
I. Se p é verdadeira e q é verdadeira, então p Λ q é verdadeira.
II. Se p é verdadeira ou q é verdadeira, então p V q é falsa.
III. Se p é verdadeira e p ⟶ q é verdadeira, então q é verdadeira.
IV. Se ~p é verdadeira e p V q é verdadeira, então q é verdadeira.
V. Se ~q é verdadeira e p ⟶ q é verdadeira, então ~p é verdadeira.
VI. Se p V q é verdadeira, p ⟶ r é verdadeira e q ⟶ r é verdadeira, então r é verdadeira.
VII. p V [q Λ (~q)]⇔ p.
VIII. p⟶ q⇔(~p) V p.
Estão INCORRETAS apenas as afirmativas
(A) I e II.
(B) II e VIII.
(C) I, II, VI e VIII.
(D) III, IV, V e VI.
Respostas
1. Resposta: Certo
2. Resposta: B
Conseguiram?
-Sim? Parabéns!
-Não? Calma não se desesperem…
Vamos lá!
1. P v (Q↔R), montando a tabela verdade temos:
2. Observe as tabelas verdades em nosso conteúdo acima, a partir disso podemos concluir que
v e v = V (I) certo
v ou f = F (II) ERRADO, logo por eliminação só nos resta a alternativa B.
Não acaba por aí, caso tenha interesse lhe sugiro a adquirir nossa apostila, clicando aqui
Que a força esteja com vocês!
E ai, gostou? Compartilha!!!
Deixe seu comentário e sugestão, queremos saber sua opinião!
Se tiver alguma sugestão de tema para abordarmos, por gentileza mande que nós escreveremos sobre. =)
Um grande abraço e bons estudos!
Fonte da imagem destacada: https://www.pictastar.com/tag/noteimporta

Somos o Instituto Maximize de Educação, uma empresa especializada na preparação de Apostilas em PDF e Cursos Online para Concursos Públicos e Vestibulares.












AS duas tabelas grandes estão erradas. Pelo menos eu procurei na internet e está diferente das suas.
Olá Celio, tudo bem? Nosso blog tem apenas a intenção de informar, não podemos nos posicionar quanto a diagnósticos médicos. Nós recomendamos que procure um profissional especializado o quanto antes. Um grande abraço e muito obrigado por seu comentário! Aproveite para nos acompanhar nas redes sociais: Facebook: https://goo.gl/fgnB61 Instagram: https://goo.gl/xe1LmU YouTube: https://goo.gl/REyOiW